Interval Calculator
Calculate musical intervals between any two notes. See semitones, frequency ratios, and consonance qualities.
How It Works
Select Notes
Choose lower and upper notes.
See Interval
View name and quality.
Learn Details
See ratios, semitones, cents.
Why Use This Tool
All Intervals
Unison through octave.
Frequency Ratios
Pure interval ratios.
Quality Info
Consonance/dissonance.
Quick Reference
All intervals at a glance.
Frequently Asked Questions
An interval is the distance between two pitches. Intervals are named by their size (2nd, 3rd, 4th, etc.) and quality (major, minor, perfect, augmented, diminished). Understanding intervals is fundamental to melody, harmony, and chord construction.
Consonant intervals (unison, octave, perfect 5th, major/minor 3rd and 6th) sound stable and pleasant. Dissonant intervals (minor 2nd, major 7th, tritone) create tension and typically resolve to consonances. Neither is "better"—both are essential in music.
The tritone (augmented 4th/diminished 5th, 6 semitones) divides the octave exactly in half. It's highly unstable and creates strong resolution tendency. In dominant 7th chords, the tritone between the 3rd and 7th drives harmonic motion toward resolution.
Chords are built from stacked intervals. A major chord = root + major 3rd + minor 3rd. A minor chord = root + minor 3rd + major 3rd. Understanding intervals lets you build any chord from first principles and analyze any voicing.
Compound intervals span more than an octave. A 9th = octave + 2nd. An 11th = octave + 4th. A 13th = octave + 6th. They're important in extended jazz chords and voice leading but reduce to their simple equivalents for analysis.
Found This Useful?
Share with fellow musicians.
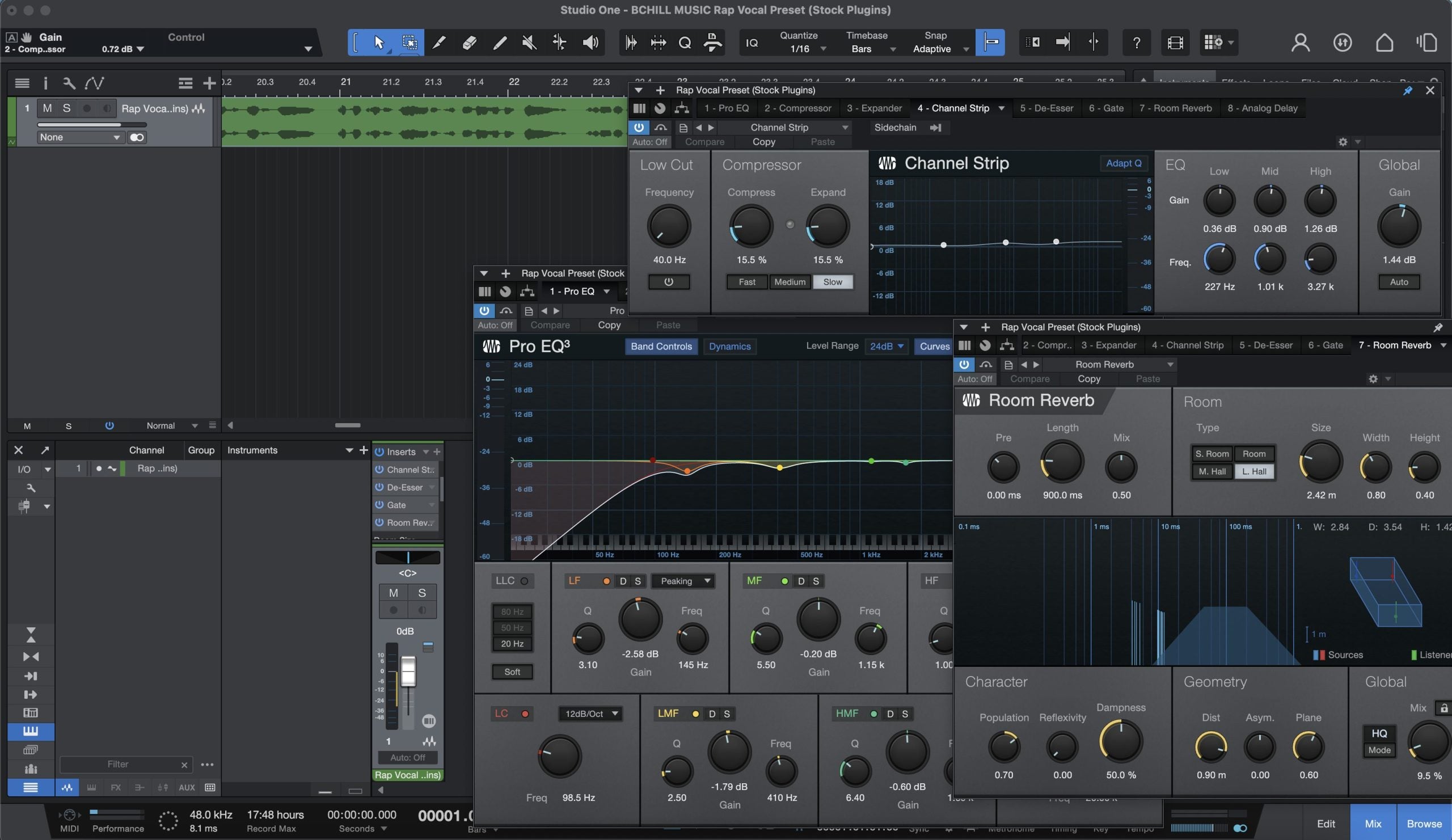
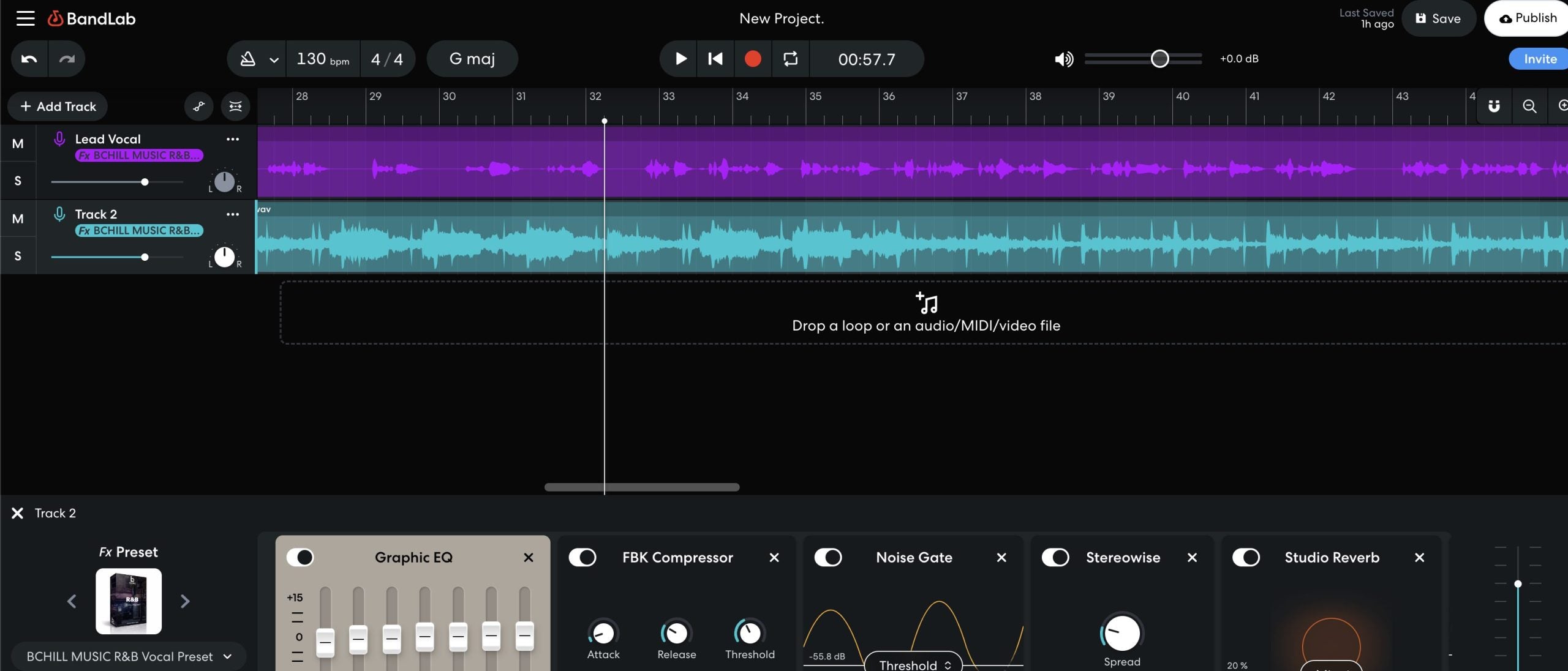
Vocal Presets & Recording Templates
Select your DAW, download, and start creating professional tracks instantly.
Type: Recording Template
Recording Template (Stock Plugins)
Type: Vocal Preset
Clear Vocals Vocal Preset (Stock Plugins)
Type: Vocal Preset
Rap Vocal Preset (Stock Plugins)
Type: Vocal Preset
R&B Vocal Preset (Stock Plugins)
Mixing & Mastering Services
Your Path To Studio-Quality Sound
Professional audio services built for artists at every level.

Mixing Services
Get your song professionally mixed for balance, clarity, and a radio-ready sound.
View Mixing Packages
Mastering Services
Finalize your mix with loudness, polish, and consistency across all platforms.
Request Mastering
Vocal Presets & Templates
Mix-ready vocal chains and recording templates for every major DAW—instant download.
Shop PresetsMusical Intervals Explained: The Foundation of Harmony and Melody
1. What Is a Musical Interval?
An interval is the distance between two pitches. When two notes sound together (harmonic interval) or one after another (melodic interval), their relationship is defined by the interval between them. This simple concept underlies all of music theory and practice.
Intervals are music's vocabulary of emotion. A perfect fifth sounds open and powerful—think the opening of "Star Wars." A minor second sounds tense and unstable—the "Jaws" theme. Learning intervals means learning the emotional language of music.
Use our Semitone Calculator to convert intervals to their semitone equivalents and vice versa.
2. Interval Naming System
Intervals have two-part names: a quality (major, minor, perfect, augmented, diminished) and a number (2nd, 3rd, 4th, etc.). Understanding this system lets you identify any interval precisely.
The Number
Count letter names from lower to upper note, including both. C to E: C(1)-D(2)-E(3) = some kind of third. C to G: C(1)-D(2)-E(3)-F(4)-G(5) = some kind of fifth. The number tells you the interval's general size.
The Quality
Quality specifies the exact size in semitones. Unisons, 4ths, 5ths, and octaves are "perfect" in their natural form. 2nds, 3rds, 6ths, and 7ths are "major" or "minor." Making a perfect interval smaller by a half step makes it "diminished"; larger makes it "augmented."
Semitone Reference
Perfect unison = 0. Minor 2nd = 1. Major 2nd = 2. Minor 3rd = 3. Major 3rd = 4. Perfect 4th = 5. Tritone = 6. Perfect 5th = 7. Minor 6th = 8. Major 6th = 9. Minor 7th = 10. Major 7th = 11. Perfect octave = 12.
3. Consonance and Dissonance
Intervals exist on a spectrum from consonant (stable, pleasant) to dissonant (unstable, tense). This classification, while somewhat subjective and culturally influenced, guides musical decision-making.
Perfect Consonances
Unison, octave, and perfect fifth are the most consonant. Their frequency ratios are simple (1:1, 2:1, 3:2), meaning their sound waves align frequently. They sound stable and restful.
Imperfect Consonances
Major and minor thirds and sixths are consonant but with more color. They're the intervals that define major vs. minor quality and provide harmonic richness without instability.
Dissonances
Seconds, sevenths, and the tritone create tension. Their complex frequency ratios produce acoustic "beating" that sounds unstable. Dissonance isn't bad—it creates movement and interest—but it typically resolves to consonance.
4. Simple Intervals
Simple intervals span one octave or less. These twelve intervals (unison through octave) form the complete basic vocabulary from which all larger intervals derive.
Perfect Intervals
Perfect unison (0 semitones): same pitch, foundational. Perfect fourth (5 semitones): stable but dependent on context. Perfect fifth (7 semitones): powerful, open, universal. Perfect octave (12 semitones): same note, higher register.
Major/Minor Intervals
Minor 2nd (1): tense, chromatic. Major 2nd (2): neutral, scalar. Minor 3rd (3): sad, minor quality. Major 3rd (4): happy, major quality. Minor 6th (8): expressive, sometimes sad. Major 6th (9): bright, optimistic. Minor 7th (10): bluesy, seeking resolution. Major 7th (11): jazzy, sophisticated tension.
The Tritone
The augmented fourth / diminished fifth (6 semitones) stands alone. It divides the octave exactly in half, creating maximum instability. Both notes want to resolve—the lower wants to rise, the upper wants to fall.
5. Compound Intervals
Compound intervals span more than an octave. They're named by adding seven to the simple interval number: a 9th is an octave plus a 2nd, an 11th is an octave plus a 4th, a 13th is an octave plus a 6th.
Common Compound Intervals
Minor 9th (13 semitones): tense, used in altered dominants. Major 9th (14): sweet, common extension. Perfect 11th (17): often raised to avoid clash with major 3rd. Minor 13th (20) / Major 13th (21): adds color to extended chords.
Character Preservation
Compound intervals generally retain the character of their simple equivalents. A major 9th sounds like a more spacious major 2nd. A perfect 11th has the quality of a perfect 4th but with different voicing implications. See our Chord Identifier to explore how these intervals function in extended chords.
6. Interval Inversion
Inverting an interval means moving the lower note up an octave (or upper note down). This creates a complementary interval that, combined with the original, spans an octave.
The Math
Original interval + inverted interval = 12 semitones (octave). Alternatively: 9 minus the interval number equals the inverted number. Major becomes minor; perfect stays perfect; augmented becomes diminished.
Examples
Major 3rd (4 semitones) inverts to minor 6th (8 semitones). Perfect 5th (7) inverts to perfect 4th (5). Minor 2nd (1) inverts to major 7th (11). The tritone (6) inverts to itself—uniquely symmetrical.
Why This Matters
Inversion knowledge helps with voice leading, understanding chord voicings, and recognizing that C-G (fifth) and G-C (fourth) are closely related. It's essential for arranging and counterpoint.
7. Interval Ear Training
Recognizing intervals by ear transforms abstract theory into practical musical skill. Trained ears hear "minor third" instantly, enabling transcription, improvisation, and deeper musical understanding.
Reference Songs
Associate each interval with a memorable song: Minor 2nd: "Jaws" theme. Major 2nd: "Happy Birthday" (first two notes). Minor 3rd: "Greensleeves" opening. Major 3rd: "When the Saints" opening. Perfect 4th: "Here Comes the Bride." Tritone: "The Simpsons" theme. Perfect 5th: "Star Wars" opening. Minor 6th: "The Entertainer." Major 6th: "NBC chime." Minor 7th: "Star Trek" theme. Major 7th: "Take On Me" (a-ha) chorus. Octave: "Somewhere Over the Rainbow."
Practice Strategies
Practice ascending and descending intervals separately—they feel different. Start with perfect intervals (easiest to identify), then add thirds and sixths, finally seconds and sevenths. Sing intervals before checking—active production beats passive recognition.
8. Intervals in Production
Interval knowledge directly improves production through better harmony creation, melody writing, and frequency management.
Creating Harmonies
Parallel thirds and sixths create smooth harmonies—common in vocal production. Parallel fifths sound powerful but "hollow" without the third—useful for rock and metal. Use our Key Transpose Calculator to find exact transposition amounts for harmony parts.
Bass and Melody Relationship
The interval between bass and melody affects perceived stability. Octaves and fifths sound solid. Thirds add warmth. Seconds, sevenths, and tritones create tension requiring resolution. Conscious interval choice between bass and lead improves arrangements.
Frequency Spacing
In mixing, intervals translate to frequency relationships. Two instruments a perfect fifth apart (frequency ratio 3:2) share more harmonics than instruments a tritone apart. Understanding this helps identify masking issues and guides EQ decisions.
Intervals are where physics meets emotion. The mathematics of frequency ratios creates the psychological experience of consonance and dissonance. Master intervals, and you master the building blocks from which all music is constructed—empowering both your analytical understanding and your creative expression.